January 20, 2025
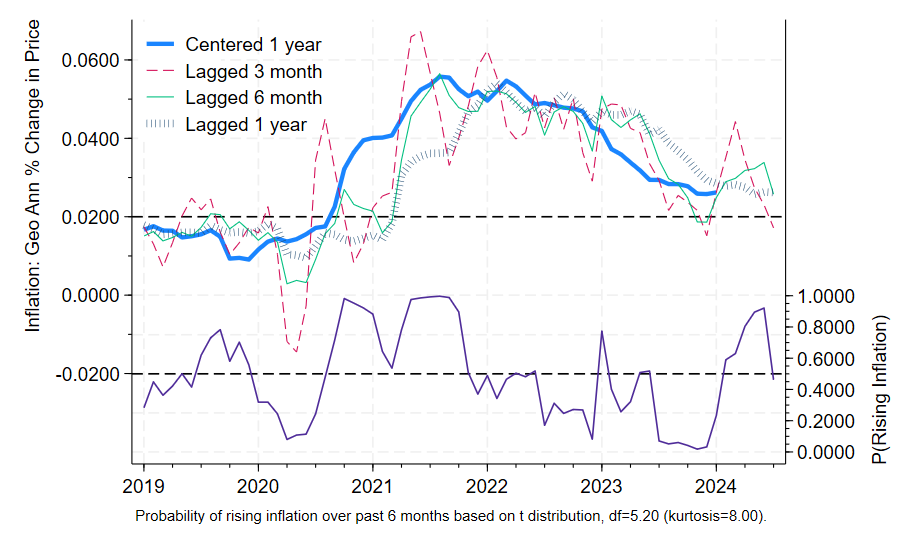
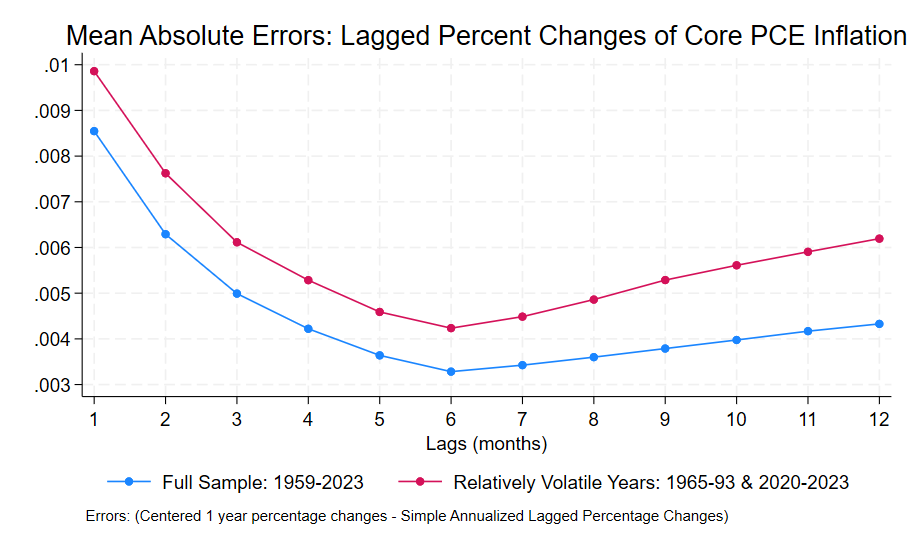
I showed a chart plotting errors for various annualized lagged percentage changes in a previous post. Here we can get an idea of what they look like. This chart from my paper shows annualized lagged percentage changes relative to underlying contemporaneous inflation as measure by the one year centered percentage change shown in the thick blue line. The red dashed line shows three month lagged percentage changes: they move around too much to provide insight into the underlying trend. The one year lagged percentage change, which is generally reported as the contemporaneous inflation rate, provides a somewhat outdated perspective (six months outdated) to existing underlying inflation. The sweet spot is in the six or seven month range: the thin green line shows the annualized six month percentage change. It fits the thick blue line visibly better than the 2 alternatives shown.
The bottom half of the chart indicates inflation’s direction, whether the centered thick blue line is rising or falling over the previous 6 months, something which is only known retrospectively. Formally, it is the probability that inflation is rising: when it is above say 80% it predicts rising inflation and when it’s below say 20% it predicts falling inflation. The probabilities are based on the price data alone. Such lack of sophistication is helpful to the extent that at least the forecast process (or rather the nowcast process) can be readily understood, unlike models where there are many contributing variables.
The data goes through July 2024 and reflects the late August report. I hope to post something more up to date soon.